Chapter 2 Solution of Ordinary Differential Equations

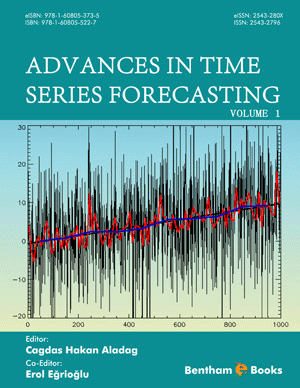
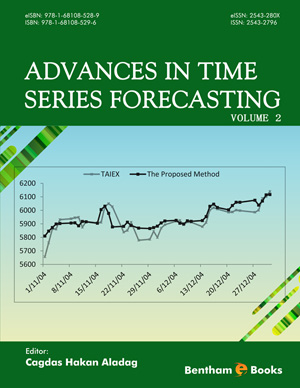
In this chapter, the linear multi step methods and Runge Kutta methods are considered. For both classes of methods, efficient algorithms have been built and implemented in Mathemat- ica. The designed Mathematica modulae are applied to selected initial value problems for ordinary differential equations and system of equations of the first order. Also, in chapter 2, an optimal algorithm has been built and implemented in the Mathematica module solveBVP. The module finds the numerical solution u = (u1, u2, , up) of the system of equations − d2u dx2 = f(x, u), a < x < b with the boundary value conditions u(a) = a0, u(b) = b0. As exercises, the equations on rotation of a heavy string and on equilibrium of a rod are solved by the module. The chapter ends with a set of questions.